分からない問題はここに書いてね458

[過去ﾛｸﾞ] 分からない問題はここに書いてね458 (1002ﾚｽ)
上下前次1-新
抽出解除ﾚｽ栞

このｽﾚｯﾄﾞは過去ﾛｸﾞ倉庫に格納されています｡
次ｽﾚ検索歴削→次ｽﾚ栞削→次ｽﾚ過去ﾛｸﾞﾒﾆｭｰ

ﾘﾛｰﾄﾞ規制です｡10分ほどで解除するので､他のﾌﾞﾗｳｻﾞへ避難してください｡

82(1): １３２人目の素数さん [] 2020/02/13(木) 01:16:35.15 ID:V8+/ESVC(5/6) AAS
>>81
解答ありがとうございます
3つのカードの差に対して大小関係を決めた上で最初が1の時（1.〜）を考えたとしても、36通りはありそうなので、だとしたら、この中のいくつかは被っているという事でしょうか？

95(1): １３２人目の素数さん [sage] 2020/02/13(木) 19:24:52.15 ID:PqkVVtQo(2/2) AAS
>>94
回答ありがとうございます
Δに出てくる単体の合併についてコンパクト近傍が取れることはどのように言えるのでしょうか

121(1): １３２人目の素数さん [sage] 2020/02/18(火) 22:52:58.15 ID:06v9pOD9(1) AAS
https://www.wolframalpha.com/input/?i=%28x-1%29%28x-2%29-x%5E9&lang=ja

298: １３２人目の素数さん [sage] 2020/02/24(月) 21:12:40.15 ID:34cHjcwm(2/2) AAS
日本語ですらないな

322: １３２人目の素数さん [sage] 2020/02/26(水) 18:02:45.15 ID:jrzfCjiF(1) AAS
>>321

log_3(a[n]) = b[n]　とおく。

　a[n+1] = a[n]^(1/4) * 3　のとき
　b[n+1] = (1/4) b[n] + 1,
　b[n+1] - 4/3 = (1/4) (b[n] - 4/3)
　　　　　　= (1/4^n) (b[1] - 4/3)
　a[n+1] = α * (a[1] /α)^(1/4^n)　→　α=3^(4/3)

　a[n+1] = a[n]^(1/8) * 3　のとき
　b[n+1] = (1/8) b[n] + 1,
　b[n+1] - 8/7 = (1/8) (b[n] - 8/7)
　　　　　　= (1/8^n) (b[1] - 8/7)
　a[n+1] = α * (a[1] /α)^(1/8^n)　→　α=3^(8/7)

x=α では y=x^(1/m) の傾き <1、吸引的
x=0 では y=x^(1/m) の傾き >1、反発的

373(2): １３２人目の素数さん [sage] 2020/03/02(月) 12:52:12.15 ID:y3F0W9KI(1/2) AAS
>>371
a:=BC=6, b:=CA=5, c:=AB=4
AH^2 = c*c + BH^2 - 2*c*BH* cos∠ABH {余弦定理}
cos∠ABH = cos∠ABD = c/BD = c/b*(b/BD)=c/b*sin∠B {正弦定理}
BH = BE*cos∠EBH = b*sin∠BDE = b*sin∠B
cos∠B = (a*a+c*c-b*b)/(2*a*b) {余弦定理}
よって
AH = sqrt(c*c + (b*b -2*c*c)*(sin∠B)^2 )
= sqrt( c*c + (b*b -2*c*c)*( 1- ((a*a+c*c-b*b)/(2*a*c))^2 ) )
= 3/16* sqrt(319) = 3.348857...

477(1): １３２人目の素数さん [] 2020/03/06(金) 15:44:30.15 ID:c2WiJIlR(1/2) AAS
>>466
((n+2)*(n +1)/2 - 3*(n/2 - 2) - 3*n - 1 )/6
= (1/12*n^2-1/2*n+1)

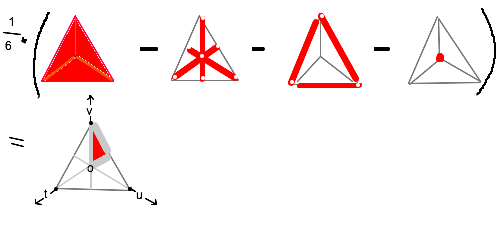
640: １３２人目の素数さん [sage] 2020/03/15(日) 08:00:20.15 ID:OTl1KJku(2/7) AAS
>>638
1 : 1/6
2 : 5/12
3 : 133/216
4 : 325/432
5 : 6541/7776
6 : 4655/5184
7 : 261493/279936
8 : 535925/559872
9 : 9796381/10077696

816(1): １３２人目の素数さん [sage] 2020/03/21(土) 19:04:04.15 ID:XWnhFsyt(20/23) AAS
>>814
＞決定番号は定義できると思うよ

そうでしょう
できないという人は、同値類を誤解してるんでしょう

＞けれど最初の問題文では
＞何に対する決定番号であるかを説明していない

説明していないのではなく、
説明を理解できていないのでしょう
理解できるまで読む必要がありますよ

＞その点をハッキリさせないと
＞上記のように言う人が居てもおかしくないのでは？

「決定番号が有限でない」という主張は
決定番号の説明が理解できないというのとは
根本的に異なる、と思いますよ

823: １３２人目の素数さん [] 2020/03/21(土) 19:20:29.15 ID:Ysr8avom(7/10) AAS
３．
問題に戻り，閉じた箱を100列に並べる.
箱の中身は私たちに知らされていないが，とにかく第l列の箱たち，第2列の箱たち第100 列の箱たちは100本の実数列S^1,S^2，・・・，S^lOOを成す(肩に乗せたのは指数ではなく添字).
これらの列はおのおの決定番号をもつ.
さて， 1〜100 のいずれかをランダムに選ぶ.
例えばkが選ばれたとせよ.
s^kの決定番号が他の列の決定番号どれよりも大きい確率は1/100に過ぎない.
　第1列〜第(k-1) 列，第(k+1)列〜第100列の箱を全部開ける.
第k列の箱たちはまだ閉じたままにしておく.
開けた箱に入った実数を見て，代表の袋をさぐり， S^1〜S^(k-l),S^(k+l)〜S100の決定番号のうちの最大値Dを書き下す.
　いよいよ第k列の(D+1) 番目から先の箱だけを開ける：S^k(D+l)， S^k(D+2)，S^k(D+3)，・・・.いま
　D >= d(S^k)
を仮定しよう.この仮定が正しい確率は99/100，そして仮定が正しいばあい，上の注意によってS^k(d)が決められるのであった.
おさらいすると，仮定のもと， s^k(D+1)，s^k(D+2)，s^k(D+3)，・・・を見て代表r＝r(s~k) が取り出せるので
列r のD番目の実数r(D)を見て，「第k列のD番目の箱に入った実数はS^k(D)＝r(D)と賭ければ，めでたく確率99/100で勝てる.
確率1-ε で勝てることも明らかであろう.
(補足)
S^k(D+l)， S^k(D+2)，S^k(D+3)，・・・：ここで^kは上付き添え字、(D+l)などは下付添え字

844(1): １３２人目の素数さん [sage] 2020/03/22(日) 07:50:24.15 ID:liILqu/N(1/6) AAS
コロナの件で疑問に思ったのだけど

無作為に１０００人を抽出してPCR検査を行ったら１０人が陽性であった。
PCR検査の感度０．７、特異度０．９として有病率の期待値と９５％信頼区間は？

有病率の事前確率分布を一様分布と仮定して検査陽性後の有病率をベータ分布で出す。
その有病率と感度・特異度をから陽性的中率を計算。
その陽性的中率を使って有病率を逆算というアルゴリズムで計算したら

> sim()
mean mode lower upper
0.010969194 0.009870096 0.005034295 0.017532847

このアルゴリズムってあってる？

上下前次1-新書関写板覧索設栞歴

ｽﾚ情報赤ﾚｽ抽出画像ﾚｽ抽出歴の未読ｽﾚ AAｻﾑﾈｲﾙ

ぬこの手ぬこTOP 0.047s